viernes, 31 de julio de 2015
¡Vacaciones! ¡Hasta finales de Agosto!
Ya
se ha dejado atrás el curso 2014-2015. Ha sido nuestro séptimo curso desde que
comenzamos el ABN y hemos tenido una actividad trepidante. La publicación de
los libros de texto ha incrementado mucho nuestro trabajo, y las tres personas
que nos hemos dedicado a ello (Concha Sánchez, José Miguel de la Rosa y yo) nos
hemos sentido muy exigidos.
Publicado por
Jaime Martínez Montero
en
16:42
3
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Noticias.
Los últimos vídeos del curso (VI)
Los alumnos de 6º del CEIP "Andalucía" no querían irse del colegio sin un nuevo vídeo que demostrara su dominio del cálculo. Como un adiós a una promoción encantadora y con la que he trabajado cuatro cursos, cierro los vídeos de este curso con estos tres (vídeos y niños). La tutora es Charo Ruiz, y la niña y los niños son Mari Carmen, Juan Marcos y Josechu. El vídeo se grabó el penúltimo día del curso.
Publicado por
Jaime Martínez Montero
en
16:39
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Resolución de Problemas.
Los últimos vídeos del curso (V).
Con estos vídeos cerré mi conferencia en el I Congreso ABN. Impresionan. Averiguan casi instantáneamente el sumatorio de los "x" primeros números. Después otra niña nos explica cómo deduce la fórmula para hacerlo. 5º del CEIP "Carlos III". Su tutora es Eva Guerrero.
Son Elo, María, Lucía, Antonio y Juan.
Son Elo, María, Lucía, Antonio y Juan.
Es Laura la que nos explica la fórmula.
Publicado por
Jaime Martínez Montero
en
16:39
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Resolución de Problemas.
Los últimos vídeos del curso (IV).
¿Cómo averiguamos cuáles son los números consecutivos si sabemos su suma? Clara nos lo enseña. Es alumna de 5º del CEIP "Carlos III", de Cádiz. La tutora es Eva Guerrero.
Publicado por
Jaime Martínez Montero
en
16:38
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Resolución de Problemas.
Los últimos vídeos del curso (III)
Alumnos de 5º del CEIP "Andalucía", de Cádiz. Una vez calculados los porcentajes, se reelaboran para adaptarlos a nuevos referentes, como son los tantos por 1, por 10, por mil y por diez mil. La tutora es Concha Sánchez. El vídeo está grabado a primeros de Junio de 2015.
Publicado por
Jaime Martínez Montero
en
16:37
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Porcentajes. 5º de Primaria.
Los últimos vídeos del curso (II).
Los alumnos de 5º de Primaria del CEIP "Andalucía", de Cádiz, componen y recomponen un problema de dos operaciones. Con ello demuestran la total comprensión del mismo. El vídeo está grabado en junio de 2015 y la tutora es Concha Sánchez.
Publicado por
Jaime Martínez Montero
en
16:37
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Resolución de Problemas.
Los últimos vídeos del curso (I).
Con este vídeo inauguré la conferencia final del I Congreso Nacional sobre Cálculo ABN. Es un estreno, en el sentido de que no lo habíamos publicado. Se grabó por la maestra (Concha Sánchez) a principios de Diciembre de 2009. Fue cuando nos dimos cuenta de la potencialidad del cálculo ABN. Uno jovencísimos Yoel, Cristian y Óscar (Los "tenores") y una preciosa Alicia (la "soprano) hacen una primera demostración del dominio del cálculo. Luego, en Abril de ese mismo curso, se grabó otro vídeo en el que ya responden a este mismo tipo de operaciones toda la clase. Por eso, si antes estos eran los tenores y la soprano, al otro vídeo lo llamamos "El Coro".
No lo pusimos en su día porque hay un error fácilmente detectable y que la docente, llevada de la emoción, no advirtió. Pero todos los delitos prescriben, así que lo hemos sacado de la cárcel.
Recordamos: alumnos del CEIP "Andalucía" de Cádiz. 2º de Primaria. Diciembre de 2009. Tutora: Concha Sánchez.
No lo pusimos en su día porque hay un error fácilmente detectable y que la docente, llevada de la emoción, no advirtió. Pero todos los delitos prescriben, así que lo hemos sacado de la cárcel.
Recordamos: alumnos del CEIP "Andalucía" de Cádiz. 2º de Primaria. Diciembre de 2009. Tutora: Concha Sánchez.
Publicado por
Jaime Martínez Montero
en
16:36
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 2º curso.
Método ABN. Desde el pasado y hacia el futuro.
Hemos dejado para cerrar el curso ABN e irnos de vacaciones la conferencia final "Método ABN. Desde el pasado y hacia el futuro" con la que Jaime Martínez Montero, cerró le I Congreso Nacional sobre algoritmos ABN celebrado en Córdoba los días 26 y 27 de Julio y que como anécdota nos regaló los prolegómenos de las sucesivas olas de calor que hemos padecido.
Por desgracia nos ha fallado el fichero del vídeo, cosas de la tecnología, pero eso no impide que os dejemos la presentación, para que una vez descargada podáis hacer clic sobre las imágenes que os llevarán a los sucesivos vídeos que han supuesto los orígenes de lo que sin lugar a duda va a suponer una revolución matemática en nuestro país.
Os agradecemos el cariño con el que nos habéis tratado este curso, los cientos de profesores y profesoras que se han añadido con ilusión a este proyecto que no quiere más que devolverle a nuestros niños y niñas la capacidad de cálculo innato que han perdido con las viejas cuentas y os esperamos el próximo curso con más ilusión si es posible.
Publicado por
Jaime Martínez Montero
en
9:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
Conferencia: "Método de aprendizaje abierto basado en números (ABN) como alternativa al método de aprendizaje cerrado basado en cifras (CBC)"
Los dos vídeos que reproducimos a continuación recoge la conferencia en el I Congreso sobre Método ABN que con el título: “Método de aprendizaje abierto basado en números (ABN) como alternativa al método de aprendizaje cerrado basado en cifras (CBC).” impartieron el Profesor Titular de la Facultad de Ciencias de la Educación (Dpto. de Psicología) Y Decano de la Facultad de Ciencias de la Educación de la Universidad de Cádiz Manuel A. García Sedeño y la Doctoranda María del Carmen Canto López que está preparando la primera tesis doctoral en ABN.
I PARTE CONFERENCIA MANUEL GARCÍA SEDEÑO
II PARTE CONFERENCIA Mª DEL CARMEN CANTO
Publicado por
Jaime Martínez Montero
en
9:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
viernes, 24 de julio de 2015
METODOLOGÍA ABN EN 3º Y 4º DE PRIMARIA.
El siguiente material corresponde al taller que la maestra de Primaria Yolanda Selma Torralbo del C.E.I.P. “José Luis Poullet" del Puerto de Santa María (Cádiz) que impartió en su taller para el Primer Ciclo de Primaria del viernes y sábado en el I Congreso sobre Método ABN.
Por problemas técnicos no disponemos de la grabación en vídeo de las intervenciones en los talleres del 2º Ciclo de Primaria, sin embargo os dejamos a continuación la documentación que presentó Yolanda Sela Torralbo en el desarrollo de su taller.
DESCARGAR: MÉTODO ABN EN SEGUNDO CICLO
DESCARGAR: ACTIVIDADES ABN PARA EL 2º CICLO
Numeración: Casa adosada 4º de Primaria
ABN 3º Invención de problema escalera descendente
ABN 3º Invención de problema escalera ascendente
ABN 3º Multiplicaciones mentales
Multiplicación decimal horizontal 4º Primaria
Multiplicaciones con euros
DIVISIONES EN 2º DE PRIMARIA
Mitades
División en 3º de Primaria
División obteniendo decimales
Divisiones obteniendo dos decimales
División mental
RESTAS MEDIDAS DE LONGITUD
SUMAS MEDIDAS DE LONGITUD
<p
SUMA NÚMEROS ROMANOS
RESTA NÚMEROS ROMANOS
MULTIPLICACIÓN NÚMEROS ROMANOS
Publicado por
Jaime Martínez Montero
en
9:22
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
jueves, 23 de julio de 2015
Uso de las regletas Cuisenaire en el método ABN
Tratamos en éste artículo el tema de las regletas Cuisenaire y su uso dentro de la metodología de cálculo ABN debido a que en numerosas ocasiones, tanto en los cursos de formación como a través de las redes sociales, se nos ha planteado su compatibilidad con el ABN.
De entrada, y más adelante lo desarrollamos, nuestra posición respecto al planteamiento de usarlas para trabajar numeración y cálculo ABN es desfavorable.
Cuando Georges Cuisenaire creó las regletas en 1952, fue con el fin de hacer algo más transparente el cálculo tradicional. Para eso nacen y para eso cumplen un papel importante dentro del algoritmo tradicional, y facilitando su comprensión el profesor Fernández Bravo hace un gran trabajo. Sin embargo el cambio metodológico del ABN, frente al cálculo tradicional, implica que la importancia que tal material puede tener en los nuevos planteamientos sea distinta, existiendo materiales muchos más eficaces y clarificadores para el alumnado, como son por ejemplo los bloques encajables o de construcción.
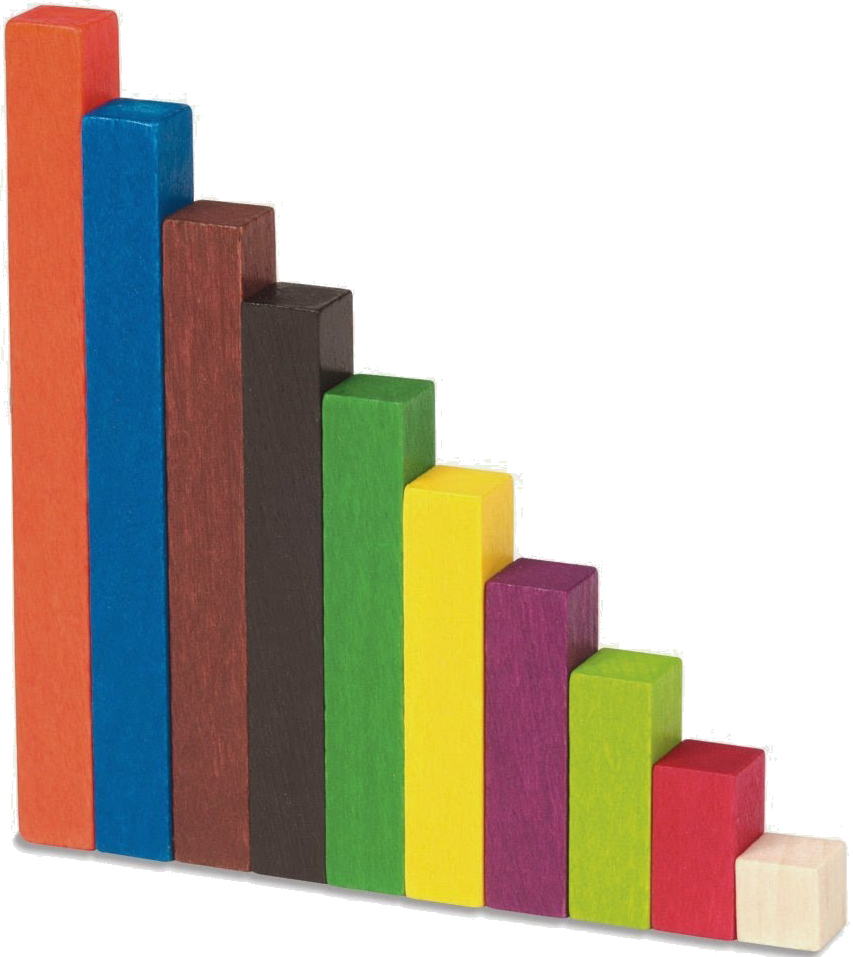
REGLETAS CUISENAIRE
Las regletas plantean, básicamente, dos problemas de “fondo”:
Las regletas se basan en medidas de longitud, no en conjuntos de elementos con su numerosidad. Los números son anteriores a las medidas. Una longitud no se puede contar. Para que sí se pueda hacer, previamente se establece un trozo de esa magnitud como unidad de referencia, y a ese trozo se le asigna un número natural, con el que ya se puede operar: iterar, detraer, comparar, etc. Según esto, primero se debe trabajar el número y el sentido numérico, y luego sus diferentes aplicaciones.
Al basarse las regletas en medidas de longitud, tan sólo es a través de ella como se pueden ver los incrementos o decrementos numéricos. Pero, ¿por qué no puede crecer o decrecer igualmente el grosor o la altura, ya que se trata de algo con volumen? ¿Se puede sostener el modelo de crecimiento o decrecimiento de las regletas como el adecuado para cualquier pareja de conjuntos que difieran entre sí un número determinado de elementos? Naturalmente que no.
También me parece un error grave identificar un número con un color. Precisamente el número de un conjunto es algo invariante, que no se ve influido por ninguna apariencia externa de las que se revistan sus elementos: color, grosor, materia, forma, etc. Nuestros alumnos de Infantil, desde los tres hasta los cinco años, se han iniciado en el sentido numérico y han conseguido una buena conceptualización numérica sin ese tipo de identificaciones.
Además de estas consideraciones de base, podemos añadir otras respecto a las equivalencias que se establecen con la regletas y la manipulación real que de las mismas realiza el niño.
Una de ellas hace referencia a la forma de contar los objetos que no depende de la forma, tamaño o color del objeto en sí, de manera que si podemos contar cualquier objeto de forma individual, ¿cómo explicamos al alumno que las regletas de distintas longitudes que representan dos, tres, cuatro,…unidades no las contamos también como objetos independientes, de la misma forma que hacemos con la unidad de referencia? P.e., cuando tenemos tres regletas de valor “dos unidades” decimos que equivale al seis, pero también podríamos decir simplemente que hay tres regletas o, dicho de otra forma, cuando nos encontramos en los primeros estadios de la cadena numérica, si le damos a un niño tres regletas de valor “dos unidades” y le pedimos que las cuente, nos responderá que hay tres, porque son tres objetos los que ve, al no tener la posibilidad de manipularlos para descomponerlos en unidades sueltas y no conocer las equivalencias para llegar a responder que hay seis unidades. Por tanto, estamos haciendo trabajar al alumnado en un ambiente confuso.
Otra cuestión hace referencia a que se trata de un material continuo, lo que impide su descomposición y su posterior composición. Con el número seis, p.e., se pueden buscar descomposiciones o composiciones equivalentes utilizando otras regletas, pero no con esa misma regleta al no poder partirla en unidades independientes. Las regletas nos permiten la equivalencia entre elementos distintos pero no la reversibilidad al no poderlas trocear y volver a componer el seis. En este aspecto, los bloques encajables o de construcción sustituyen con ventaja a las regletas, porque además de equivalencias también tienen reversibilidad, p.e., el conjunto de bloques encajables que forman el seis se puede componer y descomponer a partir de ella misma de varias formas distintas.
Una de los principales carencias del alumnado del sistema tradicional es precisamente la falta de dominio de las descomposiciones numéricas, más allá de la habitual en U, D y C, por no ser trabajadas adecuadamente tanto en su equivalencias como en su reversibilidad.
Si pasamos a la comparación de conjuntos con cardinales distintos, nos volvemos a topar con el mismo problema de equivalencias que dificulta su comprensión. P.e., comparando el seis y el nueve sólo podemos determinar la diferencia en más o en menos mediante el uso de la equivalencia con otras regletas, pero no podemos descomponer esa regleta como nueve unidades –reversibilidad- con las que poder establecer tres de ellas como la diferencia en más o menos. Esta función la realiza con excelentes resultados, y comprensión para el alumnado, los bloques encajables o mediante la comparación de ristras de tapones .
Esta falta de reversibilidad se extiende al cálculo de la suma y de la resta en sus diversos formatos tanto manipulativos como escritos mediante el algoritmo ABN, en el cual se muestra mucho más efectivo en sus primeros estadios el uso de palillos o cualquier otro material que se descomponga fácilmente de forma que lo que manipulativamente se hace, pase a su representación simbólica por escrito.
Podemos resumir que siendo la regletas un material muy adecuado para trabajar dentro del algoritmo tradicional, no es aconsejable su uso en el método ABN. Pero no porque no se pueda trabajar por parte del profesorado consciente de las limitaciones de este material, si no porque existen otro materiales, como los mencionados en el artículo, que cumplen mejor estas funciones y permiten la comprensión de una forma más natural e intuitiva.
Finalmente, insistimos en no imponer ni prohibir nada a nadie. Por otro lado, ¿cómo lo íbamos a hacer? Nuestras armas son exponer los argumentos que hay detrás de nuestras decisiones, confiando en su poder de convicción. Luego cada uno o una hace lo que considera necesario.
Publicado por
Jaime Martínez Montero
en
9:07
9
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Artículos.,
Materiales y Generadores.
martes, 21 de julio de 2015
Metodología ABN en 5º y 6º de Primaria
“METODOLOGÍA ABN EN 5º Y 6º DE PRIMARIA.” fue el taller que se presentó en el I Congreso del Método ABN por el creador del método de cálculo ABN Jaime Martínez Montero. En dicho taller se centra en el desarrollo de las operaciones de multiplicar y dividir con cifras mayores, con decimales y con redondeos, así como operaciones de con unidades de tiempo.
DESCARGAR "METODOLOGÍA ABN EN 5º Y 6º DE PRIMARIA"
DESCARGAR: "LA DIVISIÓN POR DOS CIFRAS"
Publicado por
Jaime Martínez Montero
en
11:27
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
lunes, 20 de julio de 2015
METODOLOGÍA ABN EN 1º Y 2º DE PRIMARIA.
El siguiente material corresponde al taller que la maestra de Primaria Verónica Cañete Marfil del C.E.I.P. “Santiago” de La Línea de la Concepción (Cádiz) que impartió en su taller para el Primer Ciclo de Primaria del viernes y sábado en el I Congreso sobre Método ABN.
Se trata de un material con el que realiza un recorrido por todas las operaciones básicas y las propias del algoritmo ABN, partiendo del dominio de la numeración y la descomposición numérica, pasando detenidamente por cada una de las operaciones para acabar con el cálculo con decimales en el Primer Ciclo.
Publicado por
Jaime Martínez Montero
en
8:16
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
viernes, 17 de julio de 2015
¿Cuentas? ¿Qué cuentas?... Reflexiones acerca de la aritmética escolar del siglo XXI
El siguiente vídeo recoge la conferencia inaugural del I Congreso sobre Método ABN con el título: "¿Cuentas? ¿Qué cuentas?... Reflexiones acerca de la aritmética escolar del siglo XXI" realizada por el Profesor de la Facultad de Ciencias de la Educación de Córdoba D. Rafael Bracho López.
VÍDEO CONFERENCIA INAUGURAL
Publicado por
Jaime Martínez Montero
en
10:27
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
miércoles, 15 de julio de 2015
Estrategias de formación docente en Cantabria
La comunicación "Estrategias de formación docente en Cantabria" es otra de las comunicaciones y taller que se presentaron en el I Congreso del Método ABN llevada a cabo por José Luis García González, Asesor de Formación del Centro de Formación del Profesorado de Cantabria. Entre las actividades de formación realizadas se encuentran una Web de recursos ABN, jornadas 9 horas para la “Introducción al ABN”, curso 24 horas: “ABN avanzado”, seminario de apoyo y seguimiento, además de los ampliamente solicitados cursos de formación online.
DESCARGAR: "Estrategias de formación docente en Cantabria"
VÍDEO COMUNICACIÓN
Publicado por
Jaime Martínez Montero
en
20:54
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Actividades de Formación.,
I Congreso ABN
martes, 14 de julio de 2015
Matedrez
Comunicación presentada por Mª Dolores Palmero Sánchez del CEIP “Serafines Andrades” de Chiclana de la Frontera (Cádiz), en el I Congreso sobre el Método ABN. En ella nos cuenta su experiencia con el ajedrez y las matemáticas en su curso de Segundo de Primaria, con el título de "Matedrez" combinación de matemáticas, ajedrez, creatividad y diversión. Nombre inventado por el propio alumnado y que posteriormente ha generado otros títulos como "adividrez" y "dreztectives".
En el método ABN que hemos desarrollado para la editorial Anaya, hemos reservado en todos los temas del libro de Cuarto de Primaria una página para el aprendizaje del ajedrez desde cero y hemos querido homenajearlo ilustrando el primer tema dedicado a numeración con las piezas y el mundo del ajedrez.
DESCARGAR: "MATEDREZ"
VÍDEO DE LA COMUNICACIÓN
Publicado por
Jaime Martínez Montero
en
7:31
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
lunes, 13 de julio de 2015
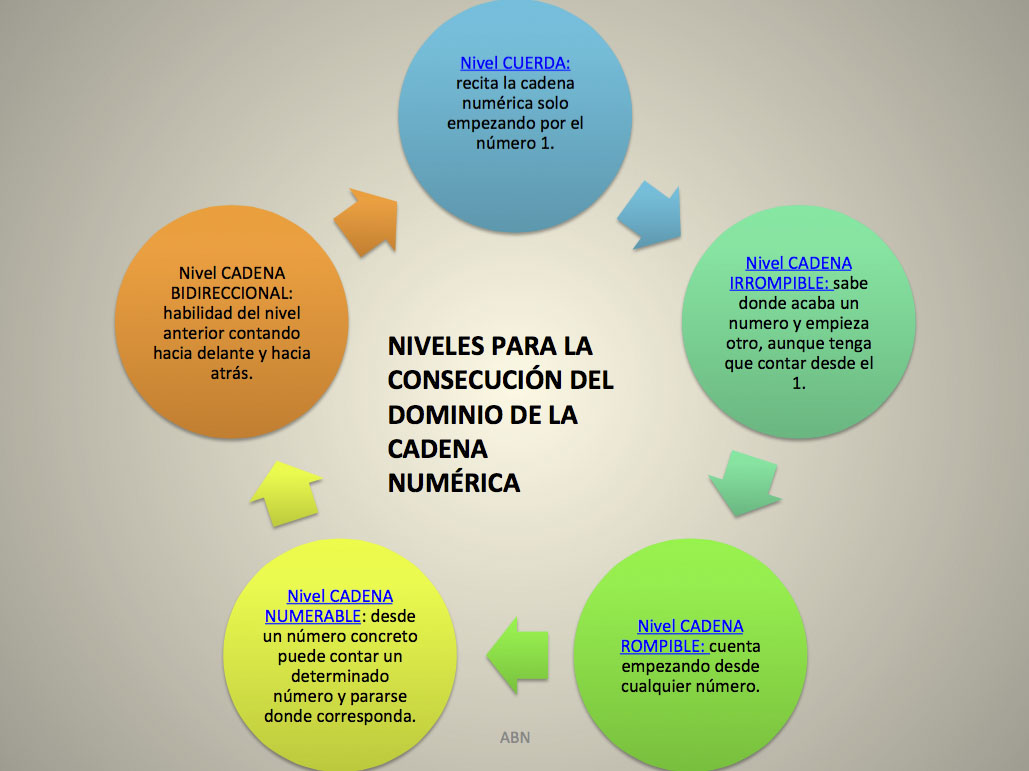
Niveles para la consecución del dominio de la cadena numérica
Comunicación "Niveles para la consecución del dominio de la cadena numérica" presentada por Irene García Martínez del Colegio “San José Esclavas" de Cádiz, en el I Congreso sobre el Método ABN.
En su intervención mostró y fue explicando las distintas etapas para a adquisición de la cadena numérica por el alumnado de Infantil objetivo fundamental en esta etapa educativa, al facilitar enormemente la compresión de aprendizajes posteriores de numeración, descomposición, composición y cálculo.
ENLACE A PRESENTACIÓN:
VÍDEO DE LA COMUNICACIÓN
Publicado por
Jaime Martínez Montero
en
8:56
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Infantil.,
I Congreso ABN
sábado, 11 de julio de 2015
Comunicaciones: Grupos interactivos ABN: “Los mayores vienen a jugar” e "Implicación y aportaciones de las familias en la implantación de la metodología ABN"
Estas dos comunicación fueron presentadas porTeresa Simonet Morales del CEIP "Serafina Andrades” de Chiclana (Cádiz). En la primero nos habló de las dificultades organizativas que conlleva el trabajo manipulativo de conteo y descomposición en Infantil, cuando se pretende trabajar en pequeño grupo y de manera más individualizada. En el segundo vídeo "Implicación y aportaciones de las familias en la implantación de la metodología ABN" nos explica la implicación de los padres y madres la implantación del algoritmo ABN en su centro.
Los problemas de organización de las actividades en Infantil los hemos resuelto, en parte, en el CEIP Serafina Andrades creando grupos interactivos de ABN con la colaboración de los tutores y alumnos de Primaria.
El mecanismos de estos grupos es el siguiente, teniendo en cuenta que existe en nuestro centro una coordinadora, la directora, que organiza las actividades de los alumnos y reparte tareas. Si no fuese así serían los tutores los que harían esta función.
- Se reúne la coordinadora con la tutora de infantil para ver las necesidades de esa semana. Ya sea conteo, numeración, descomposición, cantidad, subitización...
- Se comunica al tutor de Primaria el día y la hora que deben estar los alumnos en el aula de infantil.
- Se organizan 5 juegos, que ya previamente se han desarrollado en las asamblea durante el curso, o que son muy fáciles o muy parecidos a los que han trabajado anteriormente.
- 10 minutos antes de entrar en el aula se explican los juegos a los 5 alumnos, se les da las pautas por escrito u orales. Se recalca lo que más nos interesa que se desarrolle de cada juego.
- Se entra en el aula empiezan los juegos. Cada alumno de Primaria se responsabiliza de su juego y rota por las 5 mesas del aula de Infantil. Los juegos duran 10 minutos y están supervisados por la tutora de Infantil. Cuando termina se dice ¡CAMBIO!
- Al finalizar, los alumnos de Primaria se reúnen 5 minutos con la tutora y le informan de las dificultades o logros que han encontrado en algunos alumnos.
- La coordinadora hace una pequeña reflexión con los alumnos de qué ha fallado en los juegos y cómo se pueden mejorar.
- Reforzar las habilidades matemáticas de los alumnos de Infantil.
- Reforzar los comportamientos positivos de los alumnos de Primaria.
- Dar atención individualizada a los alumnos de Infantil.
- Explotar las posibilidades de los juegos matemáticos que tenemos en clase.
- Dar al aprendizaje un entorno lúdico. Gamificación.
Teresa Simonet Morales
Publicado por
Jaime Martínez Montero
en
19:47
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
viernes, 10 de julio de 2015
Experiencias ABN en el Aula de Integración
Comunicación presentada en el I Congreso sobre Método ABN por José Guijarro Tejada, maestro de P.T. (Pedagogía Terapéutica) en el CEIP “Alonso de Aguilar” de Aguilar de la Frontera en Córdoba, en la que cuenta mostró y explicó el proceso que ha seguido para introducir a una niña del aula específica, diagnosticada con trastorno del espectro autista, el cálculo mediante el algoritmo ABN.
La comunicación está acompañada de dos vídeos de cómo esta niña realiza una suma y una resta, de manera autónoma, mediante la adaptación de los materiales ABN.

DESARROLLO
Por lo tanto, me embarque en esta aventura, porque cuando veía a Pepe de la Rosa trabajar con sus alumnos/as, veía en ellos satisfacción y disfrute con lo que estaban haciendo y al mismo tiempo, sin ellos saberlo, aprendiendo.
Pensé que todo ese trabajo, esos materiales y esos juegos me podían servir a mí en mi aula en el trabajo diario con mis alumnos (trabajo de numeración).
Dentro de mi aula hay tres alumnos/as con NEAE (Necesidades Específicas de Apoyo Educativo): Un niño, con una discapacidad sensorial, con implante coclear y unos daños cerebrales importantes debido a las secuelas producidas por una meningitis; otro niño, con una deficiencia física, con trastorno de hiperactividad (TDH) y trastorno del espectro autista; y, por último, la niña por la que estoy aquí, con 9 años, de origen marroquí y diagnosticada con trastorno del espectro autista.
¿Por qué empecé a utilizar esta metodología?
Cuando comencé a trabajar la numeración con los niños de mi aula, utilizábamos materiales diversos y trabajábamos de forma manipulativa pero el ABN me abrió mucho más la mente y vi muchos más recursos, más materiales y más tipos de actividades para conseguir que los niños aprendieran y comprendieran los números.
Entonces empezamos a utilizar las rectas numéricas de suelo y mesa, pinzas de la ropa, barajas de cartas, tapones, tapas de toallitas, depresores, etc… y un sinfín de materiales, así como los palillos de dientes (magnífico y barato invento).
A través de ellos, esta niña comprendió que una decena equivale a diez unidades, ya que los descomponía, lo veía, vivenciaba, manipulando todo lo que estaba haciendo. Anteriormente para adquirir la decena lo intente con las regletas y el ábaco, pero el resultado fue siempre negativo, ya que la niña no entendía que una bolita roja (ábaco) o una regleta naranja equivalían a diez unidades. Ninguna las podía descomponer, las podía romper como lo hacía con los palillos.
Por lo tanto, seguimos formando números con los palillos, a descomponer en unidades y decenas, también a componerlos, tanto en la mesa como en las bandejas así como su escritura. Cuando vi que esto lo controlaba y entendía, pasamos a jugar al juego de juntar cosas. Presentamos el signo de (+) y explicamos que cada vez que lo viésemos teníamos que juntar los objetos o cosas que teníamos delante. Entonces comenzamos a hacer sumas. Como el tema de la rejilla veía que podía ser complicado lo dejé aparcado. Lo que hice entonces fue adaptar el trabajo manipulativo con los palillos y las bandejas.
En el primer vídeo cómo se puede ver, en vez de dos bandejas, nosotros utilizamos tres. Una bandeja representamos un sumando, en otra bandeja el otro sumando y una tercera bandeja donde ponemos el signo de juntar (+) y en ella juntamos los palillos de las otras dos bandejas. Entonces la niña cuenta las decenas y unidades que hay en esa bandeja y escribe el número que le ha salido. Este proceso lo empezamos con números pequeños, seguimos con números de dos cifras, con sumas fáciles “sin llevadas” y sumas más complicadas “con llevadas” aunque todos sabemos que en este método no existen las llevadas, pero para que me entendáis lo he explicado así.
De la misma manera, una vez que controla este tipo de operaciones, pasamos a trabajar las operaciones de restar. Presentamos el signo (-) y le explicamos que cada vez que lo vemos significa quitar. Comenzamos a quitar utilizando materiales y objetos y con cantidades pequeñas, ejemplo “ Tengo 9 bolitas y le quito 3, ¿cuántas me quedan?. Así poco a poco hasta que pasamos a los palillos y bandejas. Aquí también he adaptado el proceso.
En el segundo vídeo se puede observar que sólo se utiliza una sola bandeja (en las restas ABN se utilizan dos). En esa bandeja representamos el primer número (minuendo), después vemos que hacemos. Tenemos que quitar, entonces añadimos a esa misma bandeja el signo (-), y quitamos de la bandeja el segundo número (sustraendo). Contamos lo que hemos quitado. Y a continuación contamos lo que nos ha quedado en la bandeja que es el resultado final, es decir, la diferencia de los dos números.
¿Cuáles son mis próximas metas con esta niña?
Pues trabajar resta un poco más complicadas “restas llevando”, aumentar las operaciones a tres dígitos, es decir, a la centena, así como intentar pasarla a la cuadrícula, aunque no se cuando.
Mi presencia ha sido para mostrar que el algoritmo ABN, echándole un poco de imaginación y trabajo nos puede servir mucho para aquellos alumnos/as que tienen más dificultades, y que se adapta en todo momento a los ritmos y formas de aprender de nuestro alumnado.
SUMA ABN
RESTA ABN
Publicado por
Jaime Martínez Montero
en
17:46
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
Guantes para las primeras sumas
Este es otro de los materiales, idea de original de Teresa Ariza Marín del CEIP “Alonso de Aguilar” de Aguilar de la Frontera (Córdoba) y que presentó en una de sus comunicaciones en el I Congreso sobre el Método ABN.
OBJETIVO
Se trata de un material para el uso por parte del profesorado de Infantil y/o Primer Ciclo de Primaria cuyo objetivo es facilitar el aprendizaje de la suma cuando los dos sumandos son mayores de cinco. Sumas del tipo 7 + 8 que normalmente el alumnado suele tomar el mayor en la memoria, representan el menor con los dedos de sus manos y empiezan a contar los dedos desde el número que tienen memorizado.
Con este material se pretende que el alumno que trabaja la numeración ABN y que ya sabe descomponer cualquier número, vea cómo dentro de ese número que vamos a sumar se encuentra el cinco, el cual será el que irá a la memoria junto con el cinco de la descomposición del otro número que igualmente llevaremos a la memoria y formarán el 10 como complementarios o amigos del 10.
MATERIAL
- Guantes de latex
- Rotulador negro
- Números del 1 al 10 de gomaeva.
PROCEDIMIENTO
Preparamos los guantes bien pegando los números o escribiéndolos con rotulador negro. Sea de una forma u otra los números del 1 al 5 se escriben en el guante en la parte de la yema de los dedos y del 6 al 10 en la parte de las uñas. De esta forma tendremos los número del uno al cinco en una parte del guante y en la posterior del seis al diez.

Como hemos indicado anteriormente los guantes se los pone la/el maestra/o para mostrar al alumnado la forma de sumar operaciones de sumandos mayores al 5. Por ejemplo 8 + 7.
Para el 8 la/el maestra/o con los puños cerrados sin mostrar ningún número empieza a contar y a mostrar a la vez el dedo con el número que nombra. Cuando llega al cinco les dice al alumnado que ese número lo vamos a guardar en la cabeza y en ese momento cierra nuevamente la mano y la gira llevándose el puño en un gesto hacia la cabeza.
Desde esa posición, con el puño en la frente, girado y cerrado, prosigue el conteo y va sacando los dedos con el seis, siete y ocho que al haber girado la mano ahora se muestran por la parte posterior del guante.
De la misma manera procedemos con el 7 y al finalizar le preguntamos al alumnado qué números tenemos en la cabeza, a lo que nos responderán que el cinco y el cinco.
Acto seguido le decimos que de quién son amigos el cinco y el cinco, a lo que nos responderán que son amigos del diez.
Ya sólo queda mostrar y contar los dedos que tenemos abiertos en ambas manos, en una tendremos tres ya que del ocho hemos descompuesto y extraído el cinco y en la otra mano sólo tendremos dos dedos al descomponer el siete y extraer el cinco para llevárnoslo a la cabeza. Por tanto contamos o sumamos 3+2 =5 que unimos al diez para llegar a la suma final de 15.
Resumiendo todo el proceso, al final con esta actividad lo que lograremos es que partiendo de las capacidades de descomposición que ya hemos trabajado con el alumnado, extraigan el cinco de ambos números para formar el diez y que en las manos y a su vista tenga los dedos que necesitan para completar junto al diez la suma total.
La repetición de este proceso les llevará de forma natural a ver en sus mentes los números descompuestos y tomar la parte que forma decena y la que no forma decena para tras la descomposición formar el número que están sumando.
Publicado por
Jaime Martínez Montero
en
8:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
jueves, 9 de julio de 2015
Cálculo Mental en 1er Ciclo Razonado y Contextualizado
Comunicación presentada por Mª Dolores Palmero Sánchez del CEIP “Serafines Andrades” de Chiclana de la Frontera (Cádiz), en el I Congreso sobre el Método ABN. En ella realiza un análisis, evolución y ejemplificación de las bases del cálculo mental. Para ello parte de la manipulación, el trabajo de numeración, composición y descomposición y las estrategias de cálculo deribadas de la tabla de sumar y su extrapolación a las decenas y centenas.
DESCARGAR: "CÁLCULO MENTAL 1º RAZONADO Y CONTEXTUALIZADO"

Publicado por
Jaime Martínez Montero
en
19:40
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
ABN en el proyecto matemático del centro
Esta comunicación fue presentada por José Luis Silva Isla y José Mª Fuentes Jurado del “CEIP Director Manuel Somoza" de El Campillo (Sevilla). La apuesta en su centro por una nueva metodología ABN, en la enseñanza- aprendizaje de los algoritmos de las operaciones aritméticas en sustitución de los algoritmos tradicionales con los que veníamos trabajando, ha supuesto la adopción de una importante serie de medidas organizativas para que su implantación sea exitosa y prolongada en el tiempo.
Puedes oir su comunicación en el vídeo y descargar el Prezi y navegar por sus distintas pantallas para conocer más a fondo su propuesta.
DESCARGAR: "ABN EN EL PROYECTO MATEMÁTICO DEL CENTRO"

VÍDEO DE LA COMUNICACIÓN
Publicado por
Jaime Martínez Montero
en
8:22
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
martes, 7 de julio de 2015
Resolución de problemas en
Ellos inventan,
ellos entienden,
ellos resuelven.
Al entrar a clase, hay en la pizarra unos datos y el nombre de un alumno. Es el protagonista y debe, con esos datos plantear un problema, resolverlo y explicarlo a los compañeros.
Así comenzó la comunicación en el I Congreso sobre Método ABN de Mª Paz Alberola Reig del CEIP “Ausiás March” de Alicante en la que nos mostró cómo trabajan la resolución de problemas en su clase. Os dejamos un archivo en pdf de la presentación que mostró en su comunicación unos vídeos que nos muestran el desarrollo con el alumnado.
DESCARGAR: "RESOLUCIÓN DE PROBLEMAS 2º PRIMARIA"

COMUNICACIÓN DE Mª PAZ ALBEROLA REIG
VÍDEOS DE LA COMUNICACIÓN
Publicado por
Jaime Martínez Montero
en
20:42
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Primaria. 2º curso.,
I Congreso ABN
LOS ALGORITMOS ABN, ¿OTRA MANERA DE OPERAR? (Trabajo Fin de Grado)
Este nos llega desde Vigo. Para los autores y para nosotros es un orgullo publicarlo en nuestro blog.
Publicado por
Jaime Martínez Montero
en
19:14
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Documentos.
El embudo mágico
Este material, idea de original de M. Carmen Blanco Canela del CEIP "Ntra. Sra. de los Dolores" de Herrera (Sevilla), es para reforzar el concepto de decena, su formación y descomposición. Fue presentado el I Congreso sobre el Método ABN simultáneamente en dos comunicaciones, siendo la segunda comunicación impartida por Teresa Ariza Marín del CEIP "Alonso de Aguilar" de Aguilar de la Frontera (Córdoba).
Además del "embudo mágico" Mª Carmen Blanco presentó su adaptación del Payamat que publicamos recientemente y que mostramos en el vídeo de su intervención.
Material: Embudo grande de plástico, palillos sueltos y en decenas, plastilina.
Objetivo: facilitar la compresión de la formación y descomposición de números con decenas.
Procedimiento:
Este material está pensado para que el alumnado de E. Infantil, E. Especial y Primer curso de Primaria aprenda de forma lúdica la formación y descomposición de decenas. Para ello dibujamos una cara en el embudo y metemos dentro, tapando la boca de la parte estrecha, una bola de plastilina para evitar que los palillos o las decenas caigan por la boca del mismo.
Las actividades a realizar pueden ser de los siguientes tipos:
- Formación de la primera decena:
Introducimos una decena de palillos por la boca estrecha del embudo, sin ser visto por el alumnado y tapamos con la mano para evitar que se caiga. A continuación vamos contando con el alumnado los palillos y los vamos pinchando en la plastilina.dentro del embudo.
Cuando finalicemos de contar los 10 palillos decimos las palabras mágicas ¡”Badabín, badabán la decena se acaba de formar!”, y acto seguido quitamos el dedo que esté taponando la salida del embudo y dejamos caer la decena que escondimos dentro, con la sorpresa y admiración de nuestro joven público.
- Formación de decenas y unidades.
Hacemos el mismo procedimiento anterior pero escondiendo la decena y unidades del número que vayamos a contar, por ejemplo si vamos a contar e introducir 14 palillos sueltos, esconderemos en el embudo una decena y 4 palillos.
- Descomposición de decenas y unidades.
Se trata de la actividad inversa a la anterior, en este caso esconderemos palillos sueltos e introduciremos por la boca ancha del embudo el número en forma de decenas y unidades que queramos descomponer.
Conclusión:
Se trata de una actividad muy lúdica que capta la atención del alumnado, por lo que podemos adornarla con las historias fantásticas que queramos añadir. Igualmente se trata de una actividad que complementa y acompaña a otras encaminadas a la comprensión de la formación y descomposición de decenas.
Imágenes tomadas durante el curso ABN en la casa de espiritualidad juvenil de los Salesianos en Sanlúcar la Mayor (Sevilla)
PAYAMAT Y EMBUDO MÁGICO
Mª Carmen Blanco Canela
EMBUDO MÁGICO y OTROS MATERIALES
Teresa Ariza Martín
Publicado por
Jaime Martínez Montero
en
8:55
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Infantil.,
I Congreso ABN
lunes, 6 de julio de 2015
Cálculo mental para resolver contraseñas y poder entrar en clase
"Cálculo mental para resolver contraseñas y poder entrar en clase" fue una de las comunicaciones que Mª Paz Alberola Reig del CEIP "Ausiás March" de Alicante. Al final del artículo dispones de imágenes y vídeos que ilustran la comunicación.
Cada día los alumnos tienen que resolver una operación de cálculo mental para poder entrar a clase. Son operaciones variadas y fáciles de resolver: complementarios, dobles, mitades, tablas y tablas extendidas, sumas o restas, deben responderse rápidamente para evitar que se alargue demasiado el tiempo de entrada.
Solemos tardar unos 5 minutos de media. A medida que van entrando los alumnos apuntan la tarea del día en la agenda y van preparando el material necesario para la clase que se dará a continuación.
Como material se usa: las tablas del 100 pegadas en la puerta (como ayuda para el que lo necesita) y tarjetas con números u operaciones.
La contraseña es una forma de trabajar cada día el cálculo mental en dos momentos diarios, mañana y tarde, sin restar tiempo a la clase de matemáticas. Es divertido, a los alumnos les gusta hacerla y se acostumbran a pensar y responder rápidamente.


Publicado por
Jaime Martínez Montero
en
19:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN
sábado, 4 de julio de 2015
Symbaloo ABN de Berta Aguilar
Actualizacón del Symbaloo dedicado al ABN, creado por Berta Aguilar López del CEIP Teodosio de Sevilla.
Para los que no sepan qué es un Symbaloo, se trata de un tablero en la red que te ayuda a organizar todos tus contenidos de una manera fácil para navegar por internet. y en el que vas agregando todo aquello que quieres usar y compartir con otras personas.
Publicado por
José Miguel de la Rosa Sánchez
en
14:00
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Materiales y Generadores.
Algoritmos Basados en Números (ABN) 1er Ciclo
El siguiente material corresponde al taller que la maestra de Primaria Sara Herrera Ponce del CEIP "Blas Infante" de Sanlúcar de Barrameda (Cádiz) que impartió en su taller para el Primer Ciclo de Primaria del viernes y sábado en el I Congreso sobre Método ABN.
Se trata de un material con el que realiza un recorrido por todas las operaciones básicas y las propias del algoritmo ABN, partiendo del dominio de la numeración y la descomposición numérica, pasando detenidamente por cada una de las operaciones para acabar con el cálculo con decimales en el Primer Ciclo.
DESCARGAR: “Algoritmos Basados en Números (ABN) 1er Ciclo"

Publicado por
José Miguel de la Rosa Sánchez
en
12:10
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Documentos. Primer Ciclo de Primaria.,
I Congreso ABN
viernes, 3 de julio de 2015
Nueva versión de la app para el cálculo ABN
Otra de las novedades del congreso ha sido la actualización de la primera versión para móviles y tabletas Android de la app para el cálculo ABN.
La nueva versión incluye el teclado para más comodidad y evitar que al aparecer el teclado de Android tape elementos de la pantalla, también incluye todas los niveles de dificultad de producto llegando hasta factores de tres cifras por dos cifras en la rejilla ABN.
Durante los días del congreso se distribuyó gratuitamente a todos los asistentes y ya está disponible en Google play a un precio muy económico de 1,99 € que se los tiene muy merecidos Juan Carlos nuestro estupendo desarrollador de la aplicación. También está disponible una versión "libre" de prueba pero sin todas las opciones disponibles por si deseas probarla antes de descargarla.
Hemos preparado un vídeo en el que se muestran todas las funciones y tres ejemplos de operaciones.
"ENLACE APP OPERACIONES ABN EN GOOGLE PLAY"
Publicado por
José Miguel de la Rosa Sánchez
en
8:01
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN,
Materiales y Generadores.
jueves, 2 de julio de 2015
Caja para orientación y precálculo para la PDI
Son varias los rotafolios que he realizado para la pizarra digital y que tenéis disponibles en el blog. El siguiente lo presenté en el Congreso sobre Cálculo ABN y se complementa con el material que he publicado sobre la "caja para orientación y pre-cálculo" para trabajar manualmente y que permite que el alumnado de Infantil y del Primer Ciclo aprendan con más facilidad a moverse espacialmente en la rejilla ABN. Para saber el funcionamiento de éste recurso se recomienda leer previamente el artículo anteriormente mencionado.
Además y una vez alcanzada esta destreza nos permite realizar pre-cálculos de producto y división en estos niveles, con lo que el alumnado, de una forma natural, realiza ya este tipo de cálculos. Dentro del mismo programa dispones de ayuda para sacar el provecho a las distintas propuestas que os dejamos.
El archivo está realizado con el programa Activinspire de la Pizarra Digital Interactiva (PDI) Promethean, aunque puede usarse con cualquier otra, siempre que esté instalado el programa Activinspire en el ordenador. Al final del artículo os indicamos cómo descargar el fichero y el programa.
DESCARGAR: "CAJA ORIENTACIÓN Y PRECALCULO PARA LA PDI"

1.- Descargar, descomprimir y guardarlo en una carpeta que puedas localizar fácilmente.
2.- Abre el programa ActivInspire de la PDI. Para descargar ActivInspire en modo personal (gratuito) haz clic AQUÍ. Necesitas registrarte previamente.
3.- En el menú de archivo ve a “abrir” y busca en la carpeta donde lo guardaste.
4.- Descarga el archivo haciendo clic sobre la imagen.
Publicado por
José Miguel de la Rosa Sánchez
en
8:13
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
I Congreso ABN,
Materiales y Generadores.
miércoles, 1 de julio de 2015
¿En qué consiste la reforma educativa?
En clave de humor, con mucha ironía y contra los burócratas que se piensan que la clase es lo que ellos se imaginan, siete de los nueve periódicos de la Cadena Joly publicaron el 28 de Junio la Tribuna que aquí se acompaña. ¿Llevo o no llevo razón?
HAGA CLIC SOBRE LA IMAGEN PARA ACCEDER
Publicado por
Jaime Martínez Montero
en
9:19
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Artículos.
"Hacer cuentas no sirve para nada"
Este fue el reportaje que, con ocasión del I Congreso, la Cadena Joly (9 periódicos en Andalucía) publicó el pasado viernes día 26.
HAGA CLIC PARA ACCEDER
Publicado por
Jaime Martínez Montero
en
9:18
0
comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
Charlas y entrevistas.
Secuencia numeración ABN en Infantil 3 años
El siguiente material corresponde al taller que la maestra de Infantil Conchi Bonilla Arenas del CEIP Sagrado Corazón de Getafe (Madrid) y que impartió en su taller del viernes y sábado en el I Congreso sobre Método ABN.
Se trata de un material gráfico en el que se va presentando la graduación de contenidos matemáticos en Educación Infantil de 3 años mediante un descripción básica e imágenes que hablan por si mismas. Si necesitas alguna aclaración puedes hacerla en los comentarios.
DESCARGAR: "SECUENCIACIÓN NUMÉRICA ABN INF. 3 AÑOS"

Publicado por
Jaime Martínez Montero
en
7:28
1 comentarios


Enviar por correo electrónicoEscribe un blogCompartir con TwitterCompartir con FacebookCompartir en Pinterest
Etiquetas:
ABN en Infantil. 3 años.,
I Congreso ABN
Suscribirse a:
Entradas (Atom)